Thank you for your thoughtful response! I did my best to cook up a good reply, sorry if its a bit long.
Your point that we can simply “add new math” to describe new physics is intuitively appealing. However, it rests on a key assumption: that mathematical structures are ontologically separate from physical reality, serving as mere labels we apply to an independent substrate.
This assumption may be flawed. A compelling body of evidence suggests the universe doesn’t just follow mathematical laws, it appears to instantiate them directly. Quantum mechanics isn’t merely “described by” Hilbert spaces; quantum states are vectors in a Hilbert space. Gauge symmetries aren’t just helpful analogies; they are the actual mechanism by which forces operate. Complex numbers aren’t computational tricks; they are necessary for the probability amplitudes that determine outcomes.
If mathematical structures are the very medium in which physics operates, and not just our descriptions of it, then limits on formal mathematics become direct limits on what we can know about physics. The escape hatch of “we’ll just use different math” closes, because all sufficiently powerful formal systems hit the same Gödelian wall.
You suggest that if gravity doesn’t fit the Standard Model, we can find an alternate description. But this misses the deeper issue: symbolic subsystem representation itself has fundamental, inescapable costs. Let’s consider what “adding new math” actually entails:
- Discovery: Finding a new formal structure may require finding the right specific complex logical deduction path of proof making which is an often expensive, rare, and unpredictable process. If the required concept has no clear paths from existing truth knowledge it may even require non-algorithmic insight/oracle calls to create new knowledge structure connective paths.
- Verification: Proving the new system’s internal consistency may itself be an undecidable problem.
- Tractability: Even with the correct equations, they may be computationally unsolvable in practice.
- Cognition: The necessary abstractions may exceed the representational capacity of human brains.
Each layer of abstraction builds on the next (like from circles to spheres to manifolds) also carries an exponential cognitive and computational cost. There is no guarantee that a Theory of Everything resides within the representational capacity of human neurons, or even galaxy-sized quantum computers. The problem isn’t just that we haven’t found the right description; it’s that the right description might be fundamentally inaccessible to finite systems like us.
You correctly note that our perception may be flawed, allowing us to perceive only certain truths. But this isn’t something we can patch up with better math. it’s a fundamental feature of being an embedded subsystem. Observation, measurement, and description are all information-processing operations that map a high-dimensional reality onto a lower-dimensional representational substrate. You cannot solve a representational capacity problem by switching representations. It’s like trying to fit an encyclopedia into a tweet by changing the font. Its the difference between being and representing, the later will always have serious overhead limitations trying to model the former
This brings us to the crux of the misunderstanding about Gödel. His theorem doesn’t claim our theories are wrong or fallacious. It states something more profound: within any sufficiently powerful formal system, there are statements that are true but unprovable within its own axioms.
For physics, this means: even if we discovered the correct unified theory, there would still be true facts about the universe that could not be derived from it. We would need new axioms, creating a new, yet still incomplete, system. This incompleteness isn’t a sign of a broken theory; it’s an intrinsic property of formal knowledge itself.
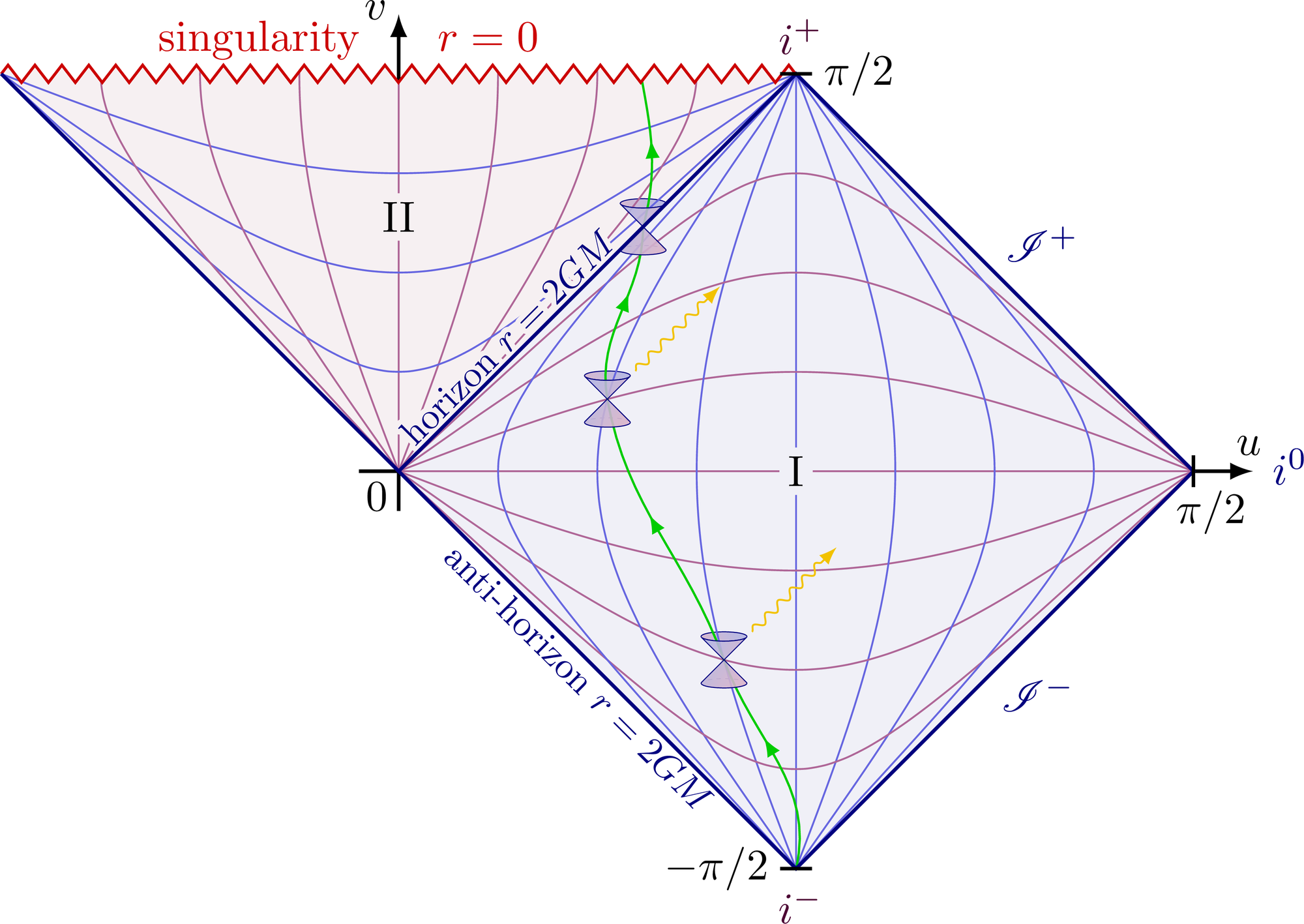
An even more formidable barrier is computational irreducibility. Some systems cannot be predicted except by simulating them step-by-step. There is no shortcut. If the universe is computationally irreducible in key aspects, then a practical “Theory of Everything” becomes a phantom. The only way to know the outcome would be to run a universe-scale simulation at universe-speed which is to say, you’ve just rebuilt the universe, not understood it.
The optimism about perpetually adding new mathematics relies on several unproven assumptions:
- That every physical phenomenon has a corresponding mathematical structure at a human-accessible level of abstraction.
- That humans will continue to produce the rare, non-algorithmic insights needed to discover them.
- That the computational cost of these structures remains tractable.
- That the resulting framework wouldn’t collapse under its own complexity, ceasing to be “unified” in any meaningful sense.
I am not arguing that a ToE is impossible or that the pursuit is futile. We can, and should, develop better approximations and unify more phenomena. But the dream of a final, complete, and provable set of equations that explains everything, requires no further input, and contains no unprovable truths, runs headlong into a fundamental barrier.





Yes I did! I spent a lot of time cooking an axiomatic framework for myself on this stuff so im happy to have the opportunity to distill my current ideas for others. Thanks! :)
The planck length and planck constant are both ultimate computational constraints on physical interactions, with planck length being the smallest meaningful scale, planck time being the smallest meaningful interval (universal framerate), and plancks constant being both combined to tell us about limits to how fast things can compute at the smallest meaningful distance steps of interaction, and ultimate bounds on how much energy we can put into physical computing.
Theres an important insight to be had here which ill share with you. Currently when people think of computation they think of digital computer transistors, turing machines, qbits, and mathematical calculations. The picture of our universe being run on an aliens harddrive or some shit like that because thats where were atas a society culturally and technologically.
Calculation is not this, or at least its not just that. A calculation is any operation that actualizes/changes a single bit in a representational systems current microstate causing it to evolve. A transistor flipping a bit is a calculation. A photon interacting with a detector to collapse its superposition is a calculation. The sun computes the distribution of electromagnetic waves and charged particles ejected. Hawking radiation/virtual particles compute a distinct particle from all possible ones that could be formed near the the event horizon.
The neurons in my brain firing to select the next word in this sentence sequence from the probabilistic sea of all things I could possibly say, is a calculation. A gravitational wave emminating from a black hole merger is a calculation, Drawing on a piece of paper a calculation actualizing a drawing from all things you could possibly draw on a paper. Smashing a particle into base components is a calculation, so is deriving a mathematical proof through cognitive operation and symbolic representation. From a certain phase space perspective, these are all the same thing. Just operations that change the current universal microstate to another iteratively flowing from one microstate bit actualization/ superposition collapse to the next. The true nature of computation is the process of microstate actualization.
Lauderes principle from classic computer science states that any classical computer transistor bit/microstate change has a certain energy cost. This can easily be extended to quantum mechanics to show every superposition collapse into a distinct qbit of information has the same actional energy cost structure directly relating to plancks constant. Essentially every time two parts of the universe interact is a computation that cost time and energy to change the universalmicrostate.
If you do a bit more digging with the logic that comes from this computation-as-actualization insight, you discover the fundamental reason why combinatorics is such a huge thing and why pascals triangle/ the binomial coefficents shows up literally everywhere in STEM. Pascals triangle directly governs the amount of microstates a finite computational phase space can access as well as the distribution of order and entropy within that phase space. Because the universe itself is a finite state representation system with 10^122 bits to form microstates, it too is governed by pascals triangle. On the 10^122th row of pascals triangle is the series of binomial coefficent distribution encoding of all possible microstates our universe can possibly evolve into.
This perspective also clears up the apparent mysterious mechanics of quantum superposition collapse and the principle of least action.
A superposition is literally just a collection of unactualized computationally accessable microstate paths a particle/ algorithm could travel through superimposed ontop of eachother. with time and energy being paid as the actional resource cost for searching through and collapsing all possible iterative states at that step in time into one definitive state. No matter if its a detector interaction ,observer interaction, or particle collision interaction, same difference. each possible microstate is seperated by exactly one single bit flip worth of difference in microstate path outcomes creating a definitive distinction between two near-equivalent states.
The choice of which microstate gets selected is statistical/combinatoric in nature. Each microstate is statistically probability weighted based on its entropy/order. Entropy is a kind of ‘information-theoretic weight’ property that affects actualization probability of that microstate based on location in pascals triangle, and its directly tied to algorithmic complexity (more complex microstates that create unique meaningful patterns of information are harder to form randomly from scratch compared to a soupy random cloud state and thus rarer).
Measurement happens when a superposition of microstates entangles with a detector causing an actualized bit of distinction within the sensors informational state. Its all about the interaction between representational systems and the collapsing of all possible superposition microstates into an actualized distinct collection of bits of information.
Plancks constant is really about the energy cost of actualizing a definitive microstate of information from a quantum superposition at smaller and smaller scales of measurement in space or time. The energy cost of distinguishing between two bits of information at a scale smaller than the planck length or at a time interval smaller than planck time will cost more energy than the universe allows in one area (it would create a kugelblitz pure energy black hole if you tried) and so any computational microstate path that differs from another with less than a plancks length worth of disctinction are indistinguishable, blurring together and creating a bedrock limit scale for computational actualization.
language is symbolic representation, cognition and conversation are computations as your neural network traces paths through your activation atlas. Our ability to talk about abstractions is tied to how complex they are to abstract about/model in our mind. The cool thing is language evolves as our understanding does so we can convey novel new concepts or perspectives that didn’t exist before.